We have seen that 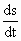is the derivative of s (t) w. r. to t and can be interpreted as the velocity.

This physical interpretation can be extended further.

If (x, y) are the co-ordinates of a moving particle then both x and y are functions of ’ t ’.

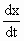, then, is the rate of change of x w. r. to ’ t ’ and 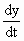is the rate of change of y w. r. to ’ t’

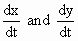since both x and y are related by a function y = f (x),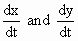 are also related. If one of is known the other can be found using the relation between these rates.

Problem of this type are known as problem of related rates.

Technique : y = f (x) where both x and y are dependent on time ' t '

Hence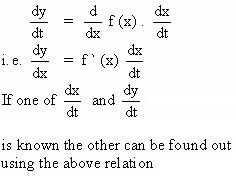

[next page]

Index

5.1 Tangent And Normal Lines
5.2 Angle Between Two Curves
5.3 Interpretation Of The Sign Of The Derivative
5.4 Locality Increasing Or Decreasing Functions 5.5 Critical Points
5.6 Turning Points
5.7 Extreme Value Theorem
5.8 The Mean-value Theorem
5.9 First Derivative Test For Local Extrema
5.10 Second Derivative Test For Local Extrema
5.11 Stationary Points
5.12 Concavity And Points Of Inflection
5.13 Rate Measure (distance, Velocity And Acceleration)
5.14 Related Rates
5.15 Differentials : Errors And Approximation

Chapter 6