| 6.4 Substitution and Change of Variables
In this method, we transform the integral to a standard form by changing the variable x of the integration to t by means of a suitable substitution of the type x = f ( t ).
Theorem : If x = f
( t ) is a differentiable function of ‘t’,
Then 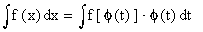
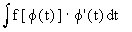
Note : Comparing 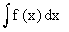 with , we observe that dx is replaced with , we observe that dx is replaced
by 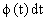 . Hence supposing
dx and dt as if they were separate entities, we have the following
working rule : . Hence supposing
dx and dt as if they were separate entities, we have the following
working rule :
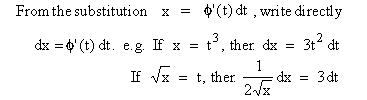
This technique is often compared with the chain - rule of derivatives since they both apply to composite functions.
Example 29
Evaluate 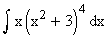
Solution : 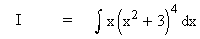
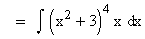
Here the inner function of the composite function 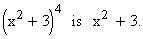
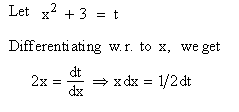
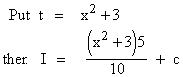
Example 30
Evaluate 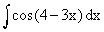
Solution : Let 4 - 3x = t,
then -3 = dt
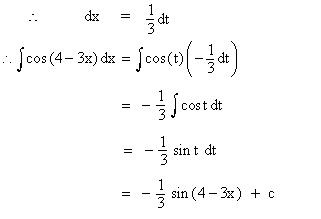
Example 31
Evaluate 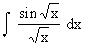
Solution : Let 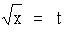
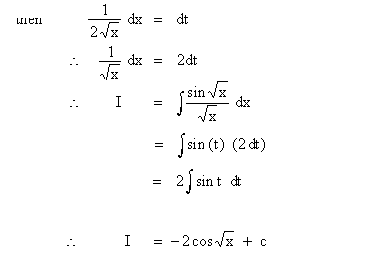
Example 32
Evaluate 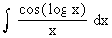
Solution : Let log x = t
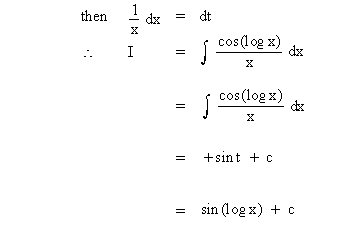
Example 33
Evaluate 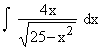
Solution : Let 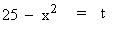
then -2 x dx = dt
\ 2x dx = -dt
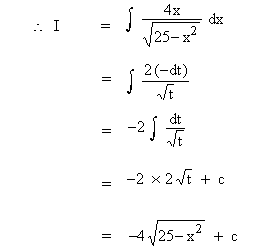
Example 34
Evaluate 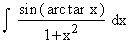
Solution : Let arc tan x = t
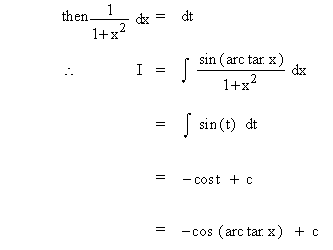
Example 35
Evaluate 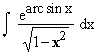
Solution : Let arc sinx = t
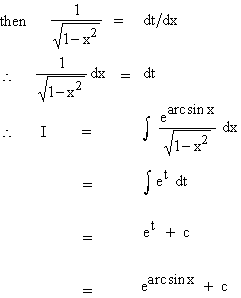
Example 36
Evaluate 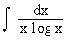 Solution : Let log x = t
Then 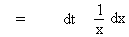
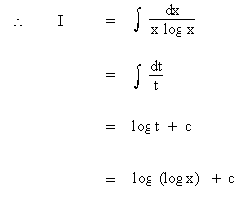
[next page]
|