|
6.6 Integration by Parts
This method is used to integrate a product, although one of the factors of the product could be unity. Also note that one of the product of functions can be easily integrable. The factors of the product will be two different kinds of functions. They will be :
1 Algebraic 2 Circular 3 Inverse circular
4 Logarithmic 5 Exponential etc.
Theorem : If u and v are functions of
x then
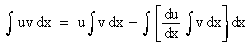
Here u is called the first function which is to be differentiated and v is the second function which is to be integrated.
Rule for the proper choice of the first function : Let us denote the various types of functions that we come across by the first alphabet i.e. L. I. A. T. E. for logarithmic, Inverse circular, Algebraic, Trigonometric (circular) and Exponential respectively. The first function to be selected will be the one which comes first in the order of the word " LIATE "
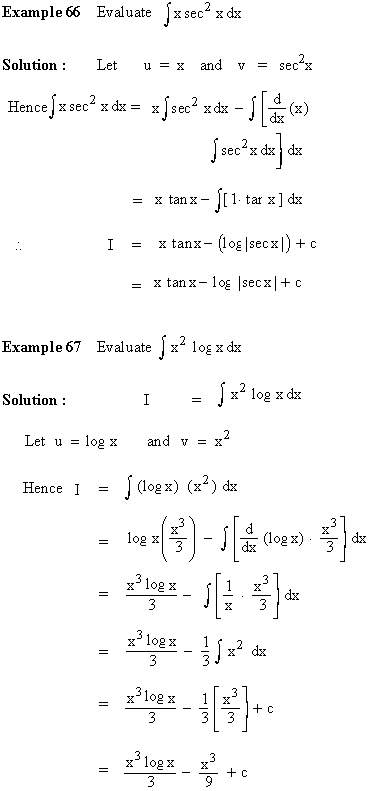 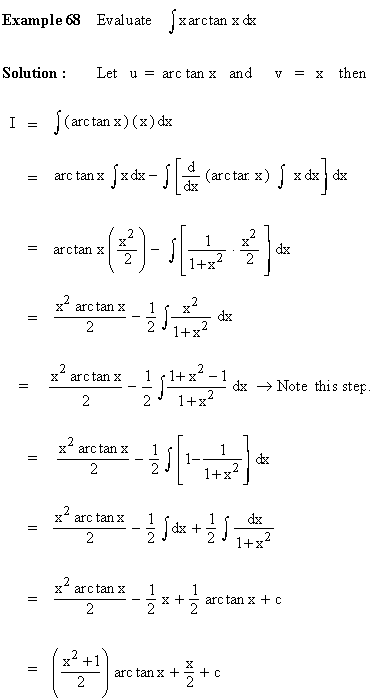
|