8.9 Errors In Testing Of Hypothesis
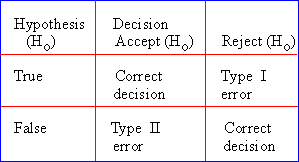
In testing any hypothesis, we get only two results : either we accept or we reject it. We do not know whether it is true or false. Hence four possibilities may arise .
- The hypothesis is true but test rejects it ( Type I error)
- The hypothesis is false but test accepts it (Type II error)
- The hypothesis is true and test accepts it ( correct decision )
- The hypothesis is false and test rejects it (correct decision)
In a statistical hypothesis testing experiment, a Type I error is committed when the null hypothesis is rejected though it is true. In terms of probability, Type I error is denoted by a (alpha) where
a = probability of type I error
= probability (rejecting Ho / Ha is true ).
A Type II error is committed by not rejecting ( i.e. accepting) the null hypothesis, when it is false. The probability of Type II error is denoted by b (beta) where
b = probability of Type - II error
= probability ( accepting Ho / Ha is false)
Now consider that the difference between two population means is actually zero i.e. Ho : m1 - m2 = 0. But our test says that the difference is significant. Here we make a Type I error.
On the other hand, suppose there is true difference between the population means i.e. Ho : m1 - m2 ¹ 0, but our test says the difference is not significant. Here we commit a Type II error.
Now suppose Murray, a manufacturer produces some type of articles of good quality. A purchaser by chance selects a sample randomly. It so happens that the sample contains many defective articles and it leads the purchaser to reject the whole product. Now, Murray suffers a loss even though he has produced a good article of quality. Therefore, this Type I error is called "producers risk".
On the other hand, if we accept the entire lot on the basis of a sample and the lot is not really good, the consumers are put in loss. Therefore, this Type II error is called the "consumers risk".
In practical situations, still other aspects are considered while accepting or rejecting a lot. The risks involved for both producer and consumer are compared. Then Type I and Type II errors are fixed; and a decision is reached.
|