Let x1i ( i = 1, 2, 3, ....., n₁ ) and x2i ( i = 1, 2, 3, ....., n₂ ) be two random independent samples drawn from two normal populations with mean m₁ and m₂ respectively but with same variance s². Let 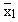and 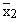be sample means and let

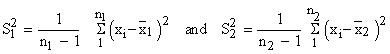
Then the static t is given by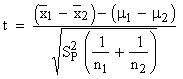

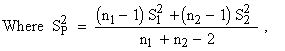is called the pooled estimate of the population variance.

Example Two types of drugs were used on 5 and 7 patients for reducing their weights in Jerry’s 'slim-beauty' health club. Drug A was allopathic and drug B was Herbal. The decrease in the weight after using drugs for six months was as follows :

Drug A :   10   12   13   11   14

Drug B :     8    9   12   14    15    10   9

Is there a significant difference in the efficiency of the two drug ? If not which drug should you buy ?

Solution:
Let the null hypothesis H_o : m₁ = m₂ or H_o : m₁ - m₂ = 0.

Alternative hypothesis H_a : m₁ ¹ m₂ or H_a : m₁ - m₂ ¹ 0

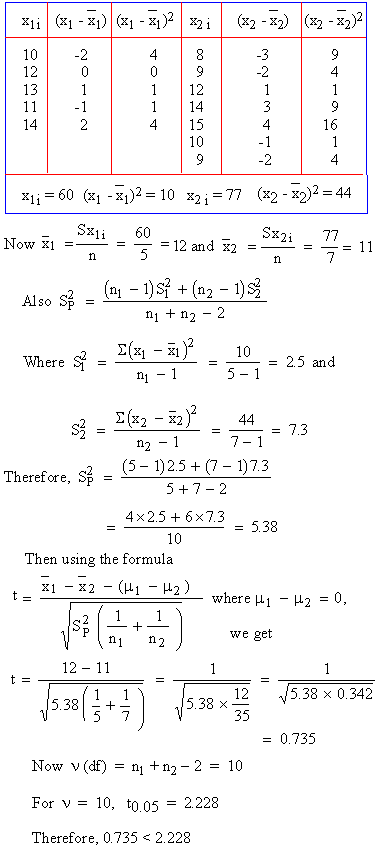
Thus the null hypothesis is accepted. Hence there is no significance in the efficiency of the two drugs. Since drug B is Herbal and there is no difference in efficiency between the two with no side effects, we should buy the Herbal drug.

Index

Chapter 1