|
Example Two types of batteries are tested
for their length of life and following results are obtained.
| |
No. of sample (n) |
Mean (x) |
Variance (s2) |
| | | | |
| Battery A |
10 |
500 hours |
100 |
| Battery B | 10 | 560 hours | 121 |
Is there a significant difference in the two batteries ?
Solution: The null hypothesis Ho
: m1
= m2
or Ho : m1
- m2
¹ 0
Alternative
hypothesis Ha
: m1
¹
m2
or Ha
: m1
- m2
¹ 0
i.e. there is no significant difference in the two batteries.
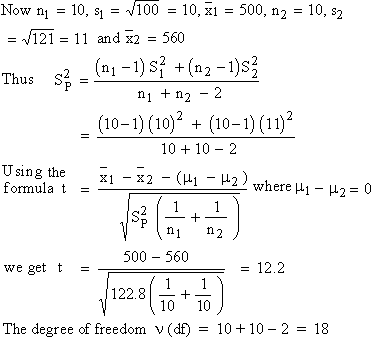
The degree of
freedom n (df) = 10 + 10
- 2 = 18
For n
= 18, t0.05
= 2.1
Therefore, 12.2 > 2.1 ( much higher )
Thus the difference is highly significant ( rejection
of Ho )
Example To test the effect of a fertilizer
on rice production, 24 equal plots of a certain land are selected.
Half of them were treated with fertilizer leaving the rest untreated.
Other conditions were the same. The mean production of rice on untreated
plots was 4.8 quintals with standard deviation of 0.4 quintal, while
the mean yield on the treated plots was 5.1 quintals with a standard
deviation of 0.36 quintal. Can we say that there is significant
improvement in the production of rice due to use of fertilizer at
0.05 level of significance ?
Solution: The null hypothesis Ho
: m1
= m2
or Ho : m1
- m2
= 0
Alternative
hypothesis Ha
: m1
¹
m2
or Ha
: m1
- m2
¹ 0
or Ha
: m1
>
m2
and the fertilizer improved the yield.
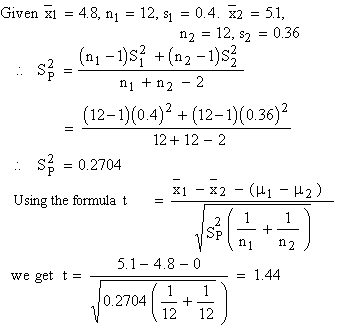
For n (df)
= 12 + 12 - 2 = 22, t0.05
= 2.07
Therefore, 1.44 < 2.07
Thus we accept Ho i.e. there is no significant
difference in rice production due to the use of fertilizer.
|