The Number line : Draw a straight line ' l '. Fix one point '0' as the origin. Let 'O' represent 'zero'. Then fix a suitable unit length. Let the point on 'l' to the right of 0 at unit distance from 0 represent the integer 1. Moving in this way further to the right of 0, we obtain points which represent integers 2, 3, 4,.... respectively. Repeat this procedure on the line left of 0, We obtain points which represent the integers -1, -2, -3..... respectively. The midpoints of each unit segment on the line 'l' and right of 0 represent the numbers In this way, all rational numbers have been represented on the line :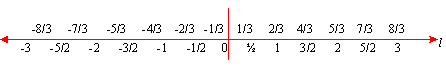 
Consider a right angled D OAB with OA = AB = 1 unit using Pythagoras theorem i.e. OB2 = OA2 + AB2 , we get OB2 = 12 + 12 i.e. OB = Ö 2 units. Therefore, if we consider a point p on the right of O at a distance OB = Ö 2 units, it represents the irrational number Ö 2 . With the same logic we can have Ö 3, Ö 5.....and it can be seen that the line contains infinitely many points which represents all irrational numbers.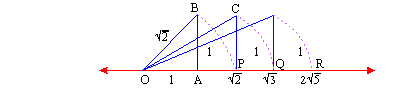 
We assume that all the rational as well as the irrational numbers have been represented on the line 'l' and there is no point left on the line 'l' which does not represent a number. Real numbers : Rational and irrational numbers taken together form the set of real numbers, denoted by R. Clearly N Í I Í Q Í R. The number line is called 'Real number line' as every real number is represented uniquely by a point on this line and conversely each point on the real number line represents a real number. Thus there is one-one correspondence between real numbers and the points on the real number line.
Properties of real numbers (axioms for real numbers) Axioms for real numbers are (1) Extend axiom (2) Field axiom (3) Order axiom (4) Completeness axiom Extend axiom : R has at least two distinct members. Field axiom : Real numbers are combined by means of two fundamental operations, which are addition and multiplication. The axioms (properties), these two operations obey are given below as the Laws of Computations. For a, b, c as real numbers 1. a + b Î R and ab Îð R ...... (Closure Law) 2. a + b = b + a and ab = ba.... (Commutative Law) 3. (a + b) + c = a + (b + c) and (a . b) . c = a . (b . c) .....(Associative law) 4. The real number 0 such that a + 0 = 0 + a = a .......(Existence of additive identity) 5. For each real number a there exists a real number (-a) such that a + (-a) = (-a) + a = 0 .......(Existence of additive inverse) 6. (a) There is a real number 1 such that a . 1 = 1. a ...........(Existence of multiplicative identity) (b) For any real number ’a’ there exists a real
number such that Simple Laws of Calculations 7. a + c = b + c Þ a = b and ac = bcð Þð ð ð a = b where c ¹ 0 8. - (-a) = a and (a-1)-1 = a where a ¹ 0 9. (- a) + (- b) = - (a + b) and (- a) (b) = - ab 10. ab = 0 Û a = 0 or b = 0 11. Additive and multiplicative identities are unique and different. 12. Additive and multiplicative inverses are unique and different. Subtraction : It is the difference between two real numbers ’a’ and ’b’ and is defined by a+(- b) and denoted by a - b. |
Introduction
Follow @Pinkmonkey_com  |
respectively. Similarly midpoints on the left 0, represent the numbers 
respectively. The points of trisection of the original unit on the right, represent the numbers 
and on the left of 0 the points of trisection shall represent the numbers 
(Existence
of multiplicative inverse)