In this method, we describe a set by specifying the properties which determines its elements uniquely.

For example

1. A is a set of all the days in a week and is written as A={x | x is a day in a week }
2. x = { x | x Î R and 5 < x <10 }
3. B = { x : x Î N and x is divisor of 70 = { 1, 2, 5, 7, 10, 14, 35, 70 }

1. The stroke ( | ) or colon ( : ) stands for 'such that'.
2. The symbol Î means belongs to . If x is an elements of the set A, then we write x Î A and read it as 'x belongs to A' or 'x is member of the set A' or 'x is an element of the set A'. Similarly the symbol Ï means does not belong to.

It is a way of pictorially describing sets. The concept was first introduced by Leonard Euler and then by Logician John Venn. We use rectangles, and circles to represent sets and one elements of the set are denoted by dots or points. For example,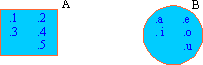

Two sets are said to be equal if they contain exactly the same elements.

For example, if X = { x | X is letter in the word ' tea' }

and Y = { y | y is a letter in the 'eat' }

Then X = Y

Now consider A = { a, b, c } and B = { 1, 2, 3 } Þ A ¹ B

The empty set

Consider a set A = { a | a Î I, 5 < x < 6 } Now note that there is no integer between 5 and 6. Therefore A has no element. We call such a set as the empty, null or void set. Thus a set which has no member is an empty set. It is denoted by f or { }. But a set { 0 } is not an empty set.

Finite sets are those whose elements are countable. They have an end.

For example A = { 1, 2, 3, 4 }.

Infinite sets are those whose elements are uncountable, they continue forever.

For example, N = { 1, 2, 3, . . . }

Index

2.1 Sets
2.2 Operations on Sets
2.3 The Algebra of Sets

Chapter 3