(A) Union of two sets : The union of two sets A and B is the set which consists of all the elements of A and all the elements of B.

Let A = { 3, 4, 6, 7 } and B = { 4, 7, 9, 10 }

then A È B = { 3, 4, 6, 7, 9, 10 }

Read A È B as A union B

Thus A È B = { x | x Î A or x Î B or both } or

A È B = { x | x belong to at least one of the sets A and B }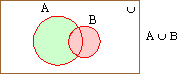

The shaded region in the above figure shows A È B.We can easily see that AÈB = BÈ A. Obviously, for any set A, A È A = A and A È f = A

(B) Intersection of two sets : The intersection of two sets A and B is the set of common elements of A and B. We write such a set as A Ç B and read it as A intersection B. Symbolically,

A Ç B = { x | x ÎA and x Î B }

For example A = { 1, 2, 3, 4 } and B = { 2, 3, 4, 5, 6, 7 }

Then A Ç B = { 2, 3, 4 }

We can easily see that for any two sets, A and B

A Ç B = B Ç A

Also note that for any set A, A Ç A = A and A Ç f = f

The sets A and B are such that (see above figure) A Ç B = f, then A and B are called as disjoint sets.

Index

2.1 Sets
2.2 Operations on Sets
2.3 The Algebra of Sets

Chapter 3