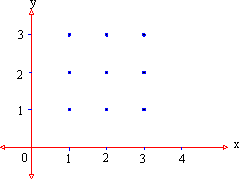
Definition : A relation is a set of ordered pairs. Notation : If R stands for the relation " is a divisor of " then we can write 6 R 30 which means 6 is a divisor of 30. If A and B are two sets, then we can say that a relation from A to B is a non empty sub set of A ´ B. Hence A R B Î A ´ B.
For example { ( 1, 1 ) , ( 1, 2 ) , ( 2, 2 ) , ( 2, 2 ) } For example { ( x, y ) | x = y Ù x Î N } Set A is a Capital of (R) Set B 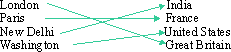
|
Index
6.1 Relations 6.2 Functions 6.3 Variation Chapter 7 |
