|
Definition 3
The absolute value | a | of a Î R is defined to be equal to 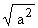 . Thus . Thus 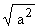 = | a | = | a |
For example (i) If a = -2 then 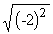 = | - 2 | = 2 = | - 2 | = 2
(ii) If a = 0 then 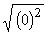 = | 0 | = 0 = | 0 | = 0
We have some simple but important results
1 ® | a - b | = | b - a |
2 ® - | a | £ a £ | a |
3 ® | a . b | = | a | . | b |
4 ® 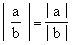
5 ® | a + b | £ | a | + | b |
6 ® | a - b | > | a | - | b |
7 ® | a + b
| > | a | - | b
|
Example 1 Solve the inequality x + 3 < 7  x Î N x Î N
Solution :
x + 3 < 7 .. ( subtracting 3 from both sides)
 x + 3 - 3 < 7 - 3 x + 3 - 3 < 7 - 3
x < 4
Example 2 Solve and graph 3 £ 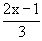 < 5 < 5
Solution :
Breaking 3 £ 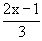 < 5 into two inequalities as < 5 into two inequalities as
3 £ 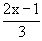 and and 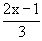 < 5 < 5
9 £ 2x - 1 and 2x - 1 < 15
9 + 1 £ 2x - 1 + 1 and 2x - 1 + 1 < 15 + 1
10 £ 2x and 2x < 16
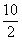 £ £ 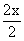 and and 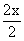 < < 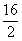
Thus the solution set is 5 £ x < 8 or [5, 8)
Graph : 
|