|
Example 6 Find the mistake from the following solution.
Suppose 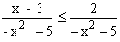
Þ x - 3 £ 2 ....[Canceling -
x2 - 5 from the denominator]
Þ x £ 5
Solution :
If a < b and c < 0, then ac > bc .....(I)
Since (- x2 - 5) < 0 then
(- x2 - 5) (-x2 - 5) Þ x - 3 ≥ 2 ....(by I)
Þ x - 3 + 3 ≥ 2 + 3 \
x ≥ 5
Example 7 Show that the following in equality is consistent
(3x + 15) > x + 5
Solution :
(3x + 15) > x + 5
Þ x + 5 > x + 5
The inequality is consistent
Example 8 If x + y > 0 and x < 2. Find the solution
for y
Solution :
x + y > 0 Þ 0 < x + y ....(1)
Also, x < 2 ....(2)
Adding (1) and (2) we get,
0 + x < x + y + 2
(Subtracting x from both the sides)
Þ 0 + x - x < x + y + 2 - x Þ 0 < y + 2
(Subtracting 2 from both the sides)
Þ 0 - 2 < y + 2 - 2
Þ - 2 < y or y > - 2
Example 9
Solve 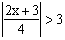
Solution :
Note that If a > 0
1) | x | = a is equal to x = a or x = - c
|