|
Example 7
If f(x) = x2- 2x + 3, x Î
R. Find the values of x for which f(x) = f (3x - 1)
Solution :
f(x) = x2 - 2x + 3 Þ f (3x - 1) = (3x - 1)2 - 2 (3x - 1) + 3
= 9x2 - 6x + 1 - 6x + 2 + 3
= 9x2 - 12 x + 6
\ f(x) = f(3x - 1) gives us
x2 - 2x + 3 = 9x2 - 12x + 6
8x2 - 10x + 3 = 0
(4x - 3) (2x - 1) = 0 ...(factorizing)
4x - 3 = 0 or 2x - 1 = 0
\ x = 3/4 or x = 1/2
\ The required values of x are 3/4 and 1/2
Example 8 An open box is to be made from a rectangular piece of tin 12 cm ´ 12 cm, by cutting four squares from each corner and turning up the sides
(1) Find the formula that expresses its volume
(2) Find the domain of the function expressing its volume
Solution :
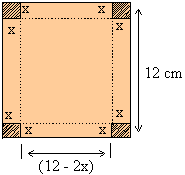
(1) Let x cm be the length of the each side of this square to be cut off and V be the volume of the box. Then the dimensions of the open box are as - Length = (12 - 2x), Breadth = (12 - 2x) and height = x in cm.
\ volume of the box (V) = Length ´ Breadth ´ Height
\ V = (12 - 2x) . (12 - 2x) . x cm3
\ V = (4x3 - 48x2 + 144x) cm3
(2) put v = 0 Þ (12 - 2x) (12 - 2x) = 0 Þ x ,= 0 or x = 6
(cut points)
|
Interval |
Test values |
Values of f(x) i.e. V |
Sign of f(x) i.e. V |
|
(- ¥ , 0) |
-1 |
(10) (10) (-1) = - 100 |
- |
|
(0, 6) |
5 |
(2) (2) (5) = 20 |
+ |
|
(6, ¥) |
7 |
(- 2) (-2) (7) = 28 |
+ |
Since the interval (6, 8) is practically impossible (say absurd), the only acceptable interval is (0, 6) i.e. the domain of V is 0 < x < 6
|