-
A rational integral function or a polynomial,
is a function of the form
a0x1 + a1xn - 1+
a2xn - 2 + .......+ an-1 +
an
where a0 , a1, a2, ......,.
a n-1 , an are constant and n is positive
integer.
A function which is a quotient of two polynomials
such as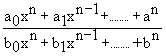
,is
called a rational function of x.
e.g.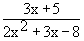 
An algebraic function is a function in
which y is expressed by an equation like
a0y n + a1yn-1
+ ..... + an = 0 where a0 a1,
......., an are rational functions of 'x'
e.g. y = (2x + p) (3x2 + q)
-
A transcendental function is a function which
is not Algebraical, Trigonometrical, exponential
and logarithmic functions are example of transcendental functions.
Thus sin x, tan-1x, ekx, log (px+q)
are transcendental functions.
-
Monotonic functions: The function y = f(x)
is monotonically increasing at a point x = a if f (a+h)
> f (a) where h >
0 (very small). But if f (a+h) <
f (a), then f(x) is decreasing at that point x = a.
The graph of such functions are always
either rises or falls.
e.g. y = sin x is monotonically increasing
in the interval
-p/2 £
x £ p/2 and decreasing in
the interval p/2 £
x £ 3p/2
-
Bounded and unbounded functions: If for all
values of x in a given interval, f(x) is never greater
than some fixed number M, the number M is called upper bound
for f(x) in that interval, whereas if f(x) is never
less than some number 'm', then m is called the lower
bound for f(x).
If f(x) has both M and m, it is called bounded,
but if one or both M or m are infinite, f(x)is called an unbounded
function.
