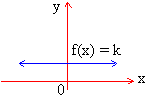13. Constant function: A function ' f ' is said to be f(x) = k, where k is constant, is called a constant funtion.

     

    e.g. f (x) = 4, then f (-2) = 4, f (0) = 4 and f (3) = 4

    The graph of this function is a straight line parallel to the x-axis.

    

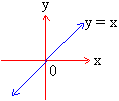
14. Identity function: The function f(x) = x is called an identity function.

    The graph of this function is a line y = x.

    It is also One-One onto.

15. Step function: Let x is a real number. We denote by the symbol [ x ], the greatest integer not greater than x

    Clearly [ 5, 3 ] = 5, [ 7 ] = 7, [-1 ] = -1, [-3.8 ] = -4. For a given real number x, [ x ] is unique. Hence we consider f(x) = [ x ]. This function is called the step function since its graph looks like steps. (For the graph of this function see the solved problem 7).

16. Inverse function: Let y = f(x). It is one-one and onto. Suppose we solve this equation and express y in terms of x say x = f (y), then f(y) is the inverse of f(x) and it is written as f ^-1, i.e. x = f ^-1 (y)

    e.g.    i)    If y = 4x - 9, then x =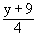

          Hence 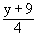is the inverse of (4x-9)

    ii)    If y = 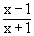then x =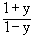

    iii)    y = tan x then x = tan^-1 y or arc tan y

    iv)    y = e^x then x = log_ey

Note that :

f : R ® R whose inverse f ^-1 exists. We know that (f^-1of) (x) = x. Thus (f ^-1of) or (f o f ^-1) are identity functions.

Index

Introduction

1.1 Functions And Mapping
1.2 Functions, Their Graphs and Classification
1.3 Rules for Drawing the Graph of a Curve
1.4 Classification of Functions
1.5 Standard Forms for the equation of a straight line
1.6 Circular Function and Trigonometry

Chapter 2