|
Example 6 Evaluate 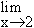
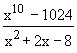
Solution : Let L = 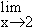
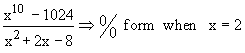
= 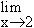
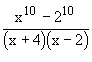

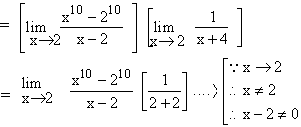
Here n = 10 and a = 2. Using above formula,
L = 10 (2)10-1 ´
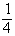
L = 10.29 ´
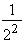
L = 10 ´ 29-2 = 10 ´ 27 = 10 ´ 128 = 1280
Example 7 Evaluate 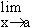
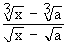
Solution : Let L = 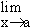
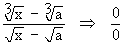 form when x = a form when x = a
\ L = 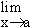
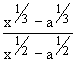
Dividing by (x-a) ¹ 0 to both numerator and denominator, we get
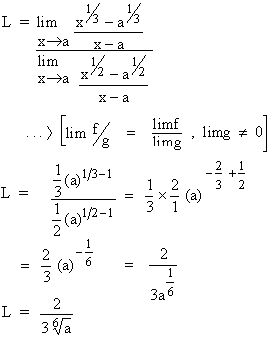
Example 8 Evaluate
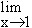 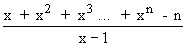
Solution : Let L = 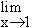
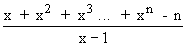
Now n = 1 + 1 + 1 + .......... n times.
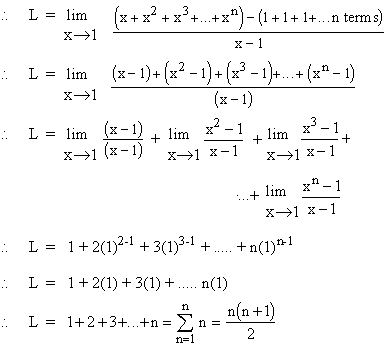
Note :
Indeterminate Form : An expression of either of the form 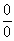 , , 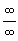 , 0, ¥, 1¥, ¥ - ¥ etc. , 0, ¥, 1¥, ¥ - ¥ etc.
The term indeterminate has become obsolete but it has relevance only when certain
expressions fall in any of the categories and they cannot be evaluated directly. These are
generally obtained by L' Hospital's rule. (Read L'Hospital's rule as Lapital's rule).
|