|
To Evaluate 
Method : Let N = numerator = a cosx
+ b sinx
D = denominator = c cosx + d sinx
We find two constants l and m such that N = l (D) + m (D’) where D' = 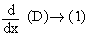
i.e. a cos x + b sin x = ( l c + m d ) cos x + ( l d - m c ) sin x. Equating co-efficients of cos x and sin x, we get \ a = (c + md) and b= (d - mc). By solving these equations, simultaneously, we obtain l and m. Putting these values in (1) we can write the given integral as :
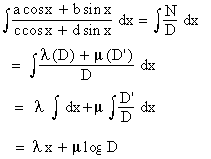
Example 44
Evaluate 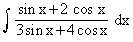
Solution : We find constants l and m
such that N = lD + mD’ ........(1)
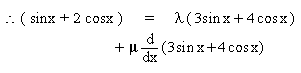
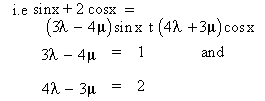
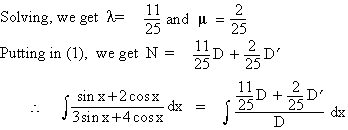
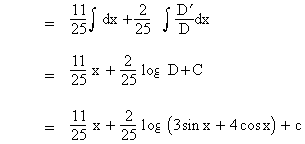
[next page]
|