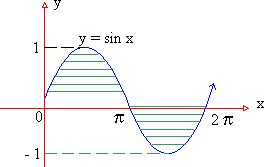
Illustration : Consider an the area, say A, bounded by the curve y = sin x, the axis of x-axis and the ordinates x = 0, x = 2p, then 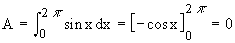This apparently absurd result due to the fact that sin x ³ 0 on [ o,p ] and sin x £ 0 on [ p, 2p ]. Hence in order to find the area in the ordinary sense of the term. We write

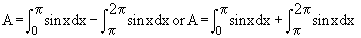
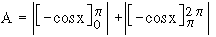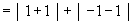
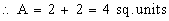
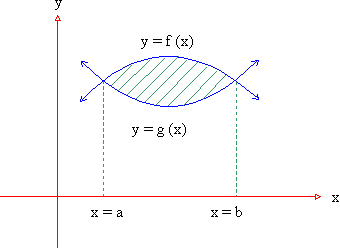
(4) Area bounded by two curves : Consider the problem of finding find the area enclosed by two curves y = f (x) and y = g (x) and the ordinates x = a and x = b . Let us assume that f (x) ³ g (x) on [ a, b] and any line parallel to y-axis from x = a to x = b intersects each curve only once. Under this situation the required area A is given by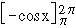

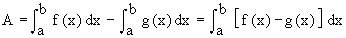
[next page]

Index

8.1 Introduction
8.2 Area
8.3 Volumes
8.4 Mean Value
8.5 Arc Length(Rectification)

Chapter 1