Example 1
LMNO is a parallelogram such that m Ð
LON = 300 and l (seg.LO)
= 12 cm. If seg.MP is the perpendicular distance between seg.LM
and seg.ON , find l (seg.MP).
Solution :
l (seg.MP) = 6
Since m Ð LON = m Ð
MNP = 300
D MNP is a 300 - 600 - 900
triangle
\ l
(seg.MP) =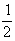 
l (seg.MN)
l (seg.MN) = l
(seg.LO) = 12 cm
\ l
seg.MP =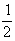
´ 12 cm
= 6 cm.
Example 2
D PQR is an acute triangle seg.PS is perpendicular to seg.QR
and seg.PT bisects QR.
Prove that l (seg.PR)2
+ l (seg.PQ)2 =
l (seg.PT)2 + l
(seg.QT)2
Solution :
To prove that l
(seg.PR)2 + l (seg.PQ)2
= l (seg.PT)2 + l
(seg.QT)2
In D PRS, by Pythagoras theorem
l (seg.PR)2 = l
(seg.PS)2 + l
(seg.SR)2
= l
(seg.PS)2 + [ l
(seg.ST) + l (seg.TR) ]2
= l
(seg.PS)2 + l (seg.ST)2+
2 l (seg.ST )
´
l (seg.TR) + l
(seg.TR) 2 ®(1)
In D PQS, by Pythagoras theorem
l (seg.PQ)2 = l
(seg.PS)2 + l (seg.QS)2
= l
(seg.PS)2 + [ l
(seg.QT) + l (seg.ST) ]2
= l
(seg.PS)2 + l (seg.QT)2
+ 2 l (seg.QT)
´
l (seg.ST) + l
(seg.ST)2 ®(2)
From (1) and (2)
l (seg.PR)2 + l
(seg.PQ)2
= l
(seg.PS)2 + l (seg.ST)2
+ 2 l (seg.ST) ´
l
(seg.TR) + l
(seg.TR)2 + l (seg.PS)2
+ l
(seg.QT)2 - 2 l
(seg.QT)
´
l (seg.ST) + l
(seg.ST)2.
Since l (seg.QT) = l
(seg.TR)
l (seg.PR)2 + l
(seg.PQ)2
= 2 l (seg.PS)2 +
2 l (seg.ST)2 + l
(seg.QT)2 + 2 l (seg.ST)
´
l (seg.QT) -
2 l (seg.ST) ´
l (seg.QT)
= 2 l (seg.PS)2 +
2 l (seg.ST)2 + 2
l (seg.QT)2
= 2 { l (seg.PS)2
+ l (seg.ST)2 } +
2 l (seg.QT)2
= 2 l (seg.PT)2 +
2 l (seg.QT)2
**********
|
