8.3 The cuboid and the cube
A book, a match box, a brick are all examples of a cuboid.
The definition of a cuboid is derived from that of the prism.
A cuboid is a solid formed by joining the corresponding vertices of two congruent rectangles such that the lateral edges are perpendicular to the planes containing the congruent rectangles. Figure 8.3 shows a cuboid.
Figure 8.3
As can be seen in Figure 8.3 the cuboid has six surfaces and each one is congruent and parallel to the one opposite to it.
Thus there is a pair of three rectangles which goes to make a cube.
It is already known that the area of a rectangle
is the product of its length and breadth, l
´ b = Area.
The surface area of a cuboid is the sum of the areas of all its faces,
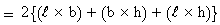
Now consider a cuboid made of 6 congruent squares
instead of a pair of three rectangles. This structure has l
= b = h i.e. the length breadth and height are the same. Such a
cuboid is called a cube.
Cube
A cube is a square right prism with the lateral edges of the same length as that of a side of the base. (See figure 8.4)
Figure 8.4 As can be seen in Figure 8.4 in a cube the length, breadth and height are equal. Therefore the surface of a cube is essentially six squares of equal length.
The area of a square is the square of its length.
The total surface area of the cube is the sum of the areas of all
its 6 surfaces. If length of one side of the cube is
l the area of one surface is
l 2
\ the surface
area of the cube = 6 ´
l
2
= 6 l
2 .
To find volume of a cuboid first a unit cube has to be defined. A unit cube is a cube with length equal to one unit.
This unit is chosen as per convenience. For small
volumes 1 cm can be chosen as the unit length . The volume of this
cube is 1 cubic cm. It is represented as 1 cm3.
For larger volumes 1 meter can be used as the unit length. In this
case the volume of the unit cube is 1 cubic meter and is represented
by 1m3 .
Depending on the size of the cuboid whose volume is to be measured the appropriate unit cube is chosen.
The volume of a cuboid is the number of unit cubes that are required to fill the cuboid completely.
Figure 8.6 shows a cuboid whose volume is to be measured. This cube has length 10 cm breadth 8 cm and height 4 cm.
The three edges OA, OB and OC are perpendicular
to each other. On these sides points LM and N are chosen such that
l (seg.
O l)
= l (seg. ON) = unit
length.
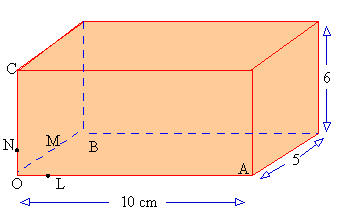Figure 8.5 These sides seg. OL, seg. OM and seg. ON form three sides of a unit cube as shown in Figure 8.6a Let another unit cube be placed on the right side of this unit cube such that one of its edges lies along seg. LA and one of its face covers the right side of the first unit cube. (See Figure 8.6b)
Figure 8.6a Figure
8.6b
Since length of seg. OA = 10 and l
(seg. OL) = 1, 10 unit cubes can
be arranged along OA. Similarly
l (seg. OB) = 5.
\ 5 unit cubes can be arranged along
seg. OB. Thus to cover the face AOBD, 10
´ 5 = 50 unit cubes will be required. They will form the
first layer towards filling the cuboid.
Since l (seg.
OC) = 6 it is obvious that 6 such layers are required to fill the
cuboid.
\ Number of unit
cubes required = 50 ´ 6
= 300
Thus the space occupied by the cuboid or its volume
= 300 cubic units
= 300 unit3
In general it may be stated that for a cuboid with
length l
, breadth b and height h the volume = l ´
b ´ h cubic units.
For a cuboid,
Surface area = 2 (l
b + b h +
l h)
Volume = (l
´ b
´ h) cubic units.
Since a cube has l
= b = c
its surface area = 6 l
2 &
Volume = l
3
|
