8.7 Sphere
The simplest example of a sphere is a ball. One can call here that a circle is a set of points in a plane that are equidistant from one point in the plane. If this is extended to the third dimension, we have all points in space equidistant from one particular point forming a sphere.
The sphere has only one surfaces and its surface
area = 4p r2
The volume of a sphere =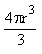
Example 1
If the lateral area of a right circular cylinder
is 24p and its radius is 2 . What is
its height.
Solution :
Lateral area of a right circular cylinder = 2 p
r h
Since r = 2 , LA = 4 p h.
Given that LA = 24 p
\ 24 p
= 4 p h
\ h = 6 units
Example 2
Find the total area of the right circular cylinder with a radius of 10 units and a height of 5 units.
Solution :
Total area of a right circular cylinder is 2prh
+ 2p r2
If r = 10 and h = 5
Total area = 100p
+ 200 p =
300 p
Example 3
What is the radius of the right circular cylinder
with volume 18p cubic units and height
= 2.
Solution :
Volume of right circular cylinder = pr2h
where r = radius and h = height
Given that V = 18p
and h = 2
\ 18p = pr2
´ 2
or r2 = 9
r = 3 units
Example 4
If the perimeter and slant height of a regular pyramid are 10 and 3 respectively. Find its lateral area.
Solution :
For a regular pyramid lateral area, LA =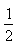 ´ p ´ l ´ p ´ l
where p = perimeter and l
= slant height
Given that p = 10 and l
= 3
\ LA = 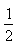 ´
10 ´ 3 = 15 square units. ´
10 ´ 3 = 15 square units.
Example 5
If the volume of a sphere is 36p.
Find its radius and surface area.
Solution :
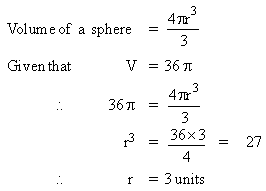
**********
|