8.4 Circular Cylinders
Pillars, pipes etc. are examples of circular cylinders encountered daily.
A circular cylinder is two circles with the same radius at a finite distance from each other with their circumferences joined.
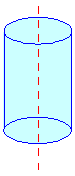
Figure 8.7 The definition of a circular cylinder is a prism with circular bases. The line joining the centers of the two circles is called the axis.
If the axis is perpendicular to the circles it is a right circular cylinder otherwise it is an oblique circular cylinder.
The lateral area of a right circular cylinder is the product of the circumference and the vertical distance between the two circles or the altitude ‘h’.
= Circumference ´
h
= 2pr
´ h
= 2 p r
h square units.
where ’r’ is the radius of the circle.
The total area must include apart from the lateral area, the areas of the two circles.
Area
of the circle = pr2
\ Area of
two circles = 2pr2
\
Total area = 2prh
+ 2pr2
= 2pr
(h + r)
= (h + r) square units
where C = circumference.
The volume of a right circular cylinder,
= area of the circle ´
height
= pr2
´ h
= pr2h
cubic units.
|