Triangle on the same base (BC) and between the same parallel lines (
l & m ) are equal in area.
We have
Ð ABC = Ð ACB - As the point D moves away from the point A, we can see that
DB + DC > AB + AC
Adding BC to both sides DB + BC + CD > AB + BC + CA
\ Perimeter of D ABC < Perimeter of D BDC
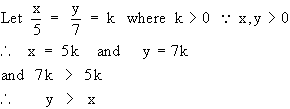
Hence B.
Questions 13 - 15 refer to the diagram.
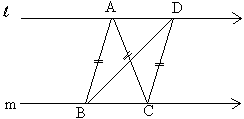
given
l || m AB = AC = DC\ A ( D ABC ) = A ( D DBC )
Hence C.
Ð ACB = alternate Ð CAD
Ð CAD = Ð ADC
and AB = AC = DC
Hence
D ABC @ D ADC By SAA or SAS Test\ A ( D ABC = A ( D ADC )
\ A ( Quad. ABCD ) = 2 A ( D ADC )
Hence C.
Hence B.