16. In a class of 140 students,

    (a) Number of boys = 60% of total is irrelevant to the solution.

    (b) 50% pass in Physics implies the other 50% fain in Physics.

    i.e. 70 pass, 70 fail.

    (c) 50% of those who passed in Physics passed in Maths as well.

    i.e. 50% of 70 or 35 students passed in Maths as well as Physics.

    (d) However there is no information about the number of students who passed in Maths from the group of 70 students who failed in Physics. Hence the total number of passes in Maths cannot be determined.

    Hence E.

17. To meet the first condition of leaving a remainder of 4 after division by 5, we add 4 to various multiples of 5 as follows:

    (a) 5 ´ 1 + 4 = 9

    (b) 5 ´ 2 + 4 = 14

    (c) 5 ´ 3 + 4 19 to obtain

    9, 14, 19, 24, 29, 34, 39 .............................. . Similarly the second condition is satisfied by adding 3 to multiples of 4 to get 7, 11, 15, 19, 23, 27, 31,................ From the above we can see that the number which satisfies both the condition will be the common number 19.

    Hence D.

18. If a + 3 = b + 5 then

    a - b = 2 and b - a = -2

    \ ( a - b )2 = 4 and ( b - a )3 = -8

    \ ( a - b )2 - ( b - a )3 = 4 - ( -8 )

    = 4 + 8

    = 12

    Hence D.

19. In right angled triangle ABC

    

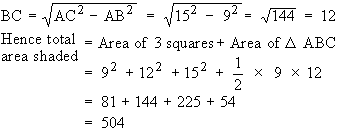
    Hence B.

     

    [next page]

Index

Test 4
Section 1 : Verbal Section
Section 2 : Quantitative Section
Section 3 : Analytical Section
Section 4 : Quantitative Section
Section 5 : Verbal Section
Section 6 : Analytical Section
Section 7 : Analytical Section
Answer key to Test 4

PART I To The Students