|
According to the class-intervals in classification the following
terms are used :
i) Class-limits : A class is formed within
the two values. These values are known as the class-limits of that
class. The lower value is called the lower limit and is denoted
by l1
while the higher value is called the upper limit of the class and
is denoted by l2.
In the example given above, the first class-interval has l1
= 0 and l2
= 10.
ii) Magnitude of the class-intervals
: The difference between the upper and lower limits of a class is
called the magnitude or length or width of a class and is denoted
by ' i ' or ' c '. Thus i º
( l2
- l1).
iii) Mid-value or class-mark : The arithmetical
average of the two class limits (i.e. the lower limit and the upper
limit ) is called the mid-value or the class mark of that class-interval.
For example, the mid-value of the class-interval ( 0 - 10 ) is
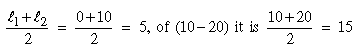 and so on. and so on.
iv) Class frequency : The units of the
data belong to any one of the groups or classes. The total number
of these units is known as the frequency of that class and is denoted
by fi or simply f. In the above example, the frequencies of the
classes in the given order are 5, 9, 32, 34 and 40 respectively.
Classification is of two types according to the class-intervals - (i) Exclusive Method
(ii) Inclusive Method.
i) Exclusive Method : In this method
the upper limit of a class becomes the lower limit of the next class.
It is called ' Exclusive ' as we do not put any item that is equal
to the upper limit of a class in the same class; we put it in the
next class, i.e. the upper limits of classes are excluded from them.
For example, a person of age 20 years will not be included in the
class-interval ( 10 - 20 ) but taken in the next class ( 20 - 30
), since in the class interval ( 10 - 20 ) only units ranging from
10 - 19 are included. The exclusive-types of class-intervals can
also be expressed as :
0 and below 10 or
0 - 9.9
10 and below 20 or 10 - 19.9
20 and below 30 or 20 - 29.9 and so on.
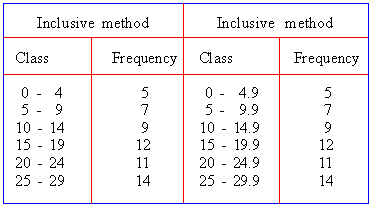
ii) Inclusive Method : In this method
the upper limit of any class interval is kept in the same class-interval.
In this method the upper limit of a previous class is less by 1
from the lower limit of the next class interval. In short this method
allows a class-interval to include both its lower and upper limits
within it. For example :
Table - 2
Class boundaries : Weights are recorded to the nearest Kg The class-intervals 60 - 62 includes all measurements from 59.50000... to 62.50000 ... Kg ; the variable being a continuous one. These numbers, indicated briefly by the exact numbers 59.5 and 62.5, are called class-boundaries or true class limits. The smaller number 59.5 is the lower class boundary and the larger one 62.5 is the upper class boundary.
In any problem if the class-intervals are given as the inclusive type, then they should first be converted into the exclusive-type . For this we require a correction factor.
Correction factor = 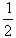 ( the upper limit of a class - the lower limit of the next class)
which is generally 0.5.
( the upper limit of a class - the lower limit of the next class)
which is generally 0.5.
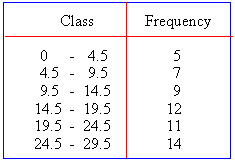
Now you subtract it from the lower limits and add it to the upper limits of the class-intervals given in the inclusive-method. The class-intervals given above can be written after correction as :
To obtain class-intervals when their mid-values are given, use the following formulae :
Lower limit (l1
) = m - i/2 and upper limit (l2
) = m + i/2
where m = mid-value and i = class-length.
|