|
6.5 Methods Of Determining Correlation
We shall consider the following most commonly used methods.(1) Scatter Plot (2) Kar Pearson’s coefficient of correlation (3) Spearman’s Rank-correlation coefficient.
1) Scatter Plot ( Scatter diagram or dot diagram ):
In this method the values of the two variables are plotted on a
graph paper. One is taken along the horizontal ( (x-axis) and the
other along the vertical (y-axis). By plotting the data, we get
points (dots) on the graph which are generally scattered and hence
the name ‘Scatter Plot’.
The manner in which these points are scattered, suggest the degree and the direction of correlation. The degree of correlation is denoted by ‘ r ’ and its direction is given by the signs positive and negative.
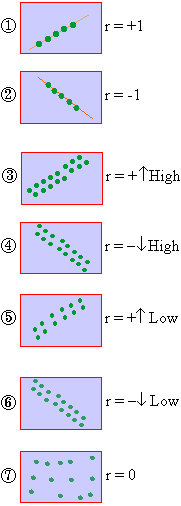i) If all points lie on a rising straight line the correlation is perfectly positive and r = +1 (see fig.1 )
ii) If all points lie on a falling
straight line the correlation is perfectly negative and r = -1 (see
fig.2)
iii) If the points lie in narrow strip, rising upwards, the correlation is high degree of positive (see fig.3)
iv) If the points lie in a narrow strip, falling downwards, the correlation is high degree of negative (see fig.4)
v) If the points are spread widely over a broad strip, rising upwards, the correlation is low degree positive (see fig.5)
vi) If the points are spread widely over a broad strip, falling downward, the correlation is low degree negative (see fig.6)
vii) If the points are spread (scattered) without any specific pattern, the correlation is absent. i.e. r = 0. (see fig.7)
Though this method is simple and is a rough idea
about the existence and the degree of correlation, it is not reliable.
As it is not a mathematical method, it cannot measure the degree
of correlation.
2) Karl Pearson’s coefficient of correlation:
It gives the numerical expression for the measure of correlation.
it is noted by ‘ r ’. The value of ‘ r ’ gives the magnitude of
correlation and sign denotes its direction. It is defined as
r =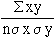 
where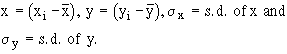 
N = Number of pairs of observation
|
