|
6.9 Linear Regression
Correlation gives us the idea of the measure of magnitude and direction between correlated variables. Now it is natural to think of a method that helps us in estimating the value of one variable when the other is known. Also correlation does not imply causation. The fact that the variables x and y are correlated does not necessarily mean that x causes y or vice versa. For example, you would find that the number of schools in a town is correlated to the number of accidents in the town. The reason for these accidents is not the school attendance; but these two increases what is known as population. A statistical procedure called regression is concerned with causation in a relationship among variables. It assesses the contribution of one or more variable called causing variable or independent variable or one which is being caused (dependent variable). When there is only one independent variable then the relationship is expressed by a straight line. This procedure is called simple linear regression.
Regression can be defined as a method that
estimates the value of one variable when that of other variable
is known, provided the variables are correlated. The dictionary
meaning of regression is "to go backward." It was used
for the first time by Sir Francis Galton in his research paper "Regression
towards mediocrity in hereditary stature."
Lines of Regression: In scatter plot, we
have seen that if the variables are highly correlated then the points
(dots) lie in a narrow strip. if the strip is nearly straight, we
can draw a straight line, such that all points are close to it from
both sides. such a line can be taken as an ideal representation
of variation. This line is called the line of best fit if it minimizes
the distances of all data points from it.
This line is called the line of regression. Now prediction is easy because now all we need to do is to extend the line and read the value. Thus to obtain a line of regression, we need to have a line of best fit. But statisticians donít measure the distances by dropping perpendiculars from points on to the line. They measure deviations ( or errors or residuals as they are called) (i) vertically and (ii) horizontally. Thus we get two lines of regressions as shown in the figure (1) and (2).
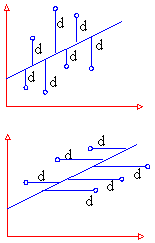
(1) Line of regression of y on x
Its form is y = a + b x
It is used to estimate y when x is given
(2) Line of regression of x on y
Its form is x = a + b y
It is used to estimate x when y is given.
They are obtained by (1) graphically - by Scatter plot (ii) Mathematically - by the method of least squares.
|