6.7 Probable Error

It is used to help in the determination of the Karl Pearson’s coefficient of correlation ‘ r ’. Due to this ‘ r ’ is corrected to a great extent but note that ‘ r ’ depends on the random sampling and its conditions. it is given by

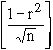
1. If the value of r is less than P. E., then there is no evidence of correlation i.e. r is not significant.

2. If r is more than 6 times the P. E. ‘ r ’ is practically certain .i.e. significant.

3. By adding or subtracting P. E. to ‘ r ’ , we get the upper and Lower limits within which ‘ r ’ of the population can be expected to lie.

   Symbolically e = r ± P. E.

   P = Correlation ( coefficient ) of the population.

Example If r = 0.6 and n = 64 find out the probable error of the coefficient of correlation.

Solution: P. E. = 0.6745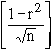

= 0.6745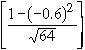

=

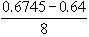
= 0.57

Index

6. 1 Introduction
6. 2 Correlation
6. 3 Types of Correlation
6. 4 Degrees of Correlation
6. 5 Methods of determining correlation
6. 6 Coefficients of Correlation for Bivariate Grouped Data
6. 7 Probable Error
6. 8 Rank Correlation Coefficient
6. 9 Linear Regression