|
CHAPTER 1 : CIRCULAR FUNCTIONS AND TRIGONOMETRY
The word Trigonometry is derived from two Greek
words - 'trigon' (meaning a triangle) and `metron' (meaning a measure)
and hence literally Trigonometry means the measurement of a triangle.
Thus it is that branch of mathematics which deals with the measurement
of the sides and angles of a triangle and the investigation of various
relations which exist among them.
1.1 Angles (Radians and Degrees)

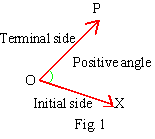
Note that the definition says "an angle".
This is because in the given configuration the initial side may
be rotated clock-wise or counter clockwise, and it may be rotated
completely around once or several times before resting at the terminal
side.
Following figure shows a few of angles determined
by same configuration.
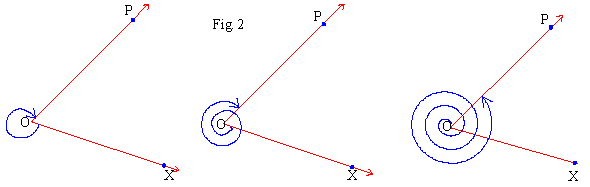
Click here to enlarge
An angle so generated is called positive (+ve)
if the direction of rotation (indicated by curved arrows) is counter
clockwise and negative (-ve) if the direction of rotation is clockwise.
(2) Zero angle and straight angle : If the ray
OX does not rotate at all i.e. ray OP coincides with OX without
rotation then ÐXOP is a zero angle.
When rotation takes place, the angle so formed can be measured in
terms of the amount of rotation. One full rotation in counter clockwise
sense describes an angle of 3600 of Sexagesimal system
(or the English System). Hence, one half of complete rotation is
the angle of 1/2 (3600 ). This angle is called straight
angle since ray OX and OP are in straight line but in the opposite
direction.
|