|
CHAPTER 2 : TRIGONOMETRIC FUNCTIONS OF ACUTE ANGLES
2.1 Trigonometric Ratios of Acute Angles
The building blocks of trigonometry is the characteristics of similar triangles, originally formulated by 'Euclid'.
If two corresponding angles are congruent then the two triangles are similar. Also corresponding sides of two similar triangles preserve the same ratio. This idea leads to the trigonometric ratios. For trigonometric ratios of acute angles, we need right angled triangles. The measure of an acute angle in a right angled triangle, lower case Greek letters a and q are usually used.
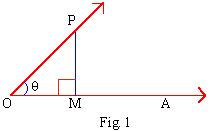
Let a revolving line OP starts from OA and revolve into a position OP, thus tracing out the angle AOP. Draw seg PM, perpendicular to the initial line OA. Let Ð POM = q.
In the right angled triangle POM, OP is the hypotenuse, PM
is the opposite side of q and OM is the
adjacent side of q. Now trigonometric
ratios, or functions are relation between any two sides of a right
angle triangle with respect to a given angle. Thus a trigonometric
ratio is a function of an angle.
The trigonometric ratios of Ð POM = q are defined as follows :

Click here to enlarge
It should be noted that the trigonometric ratios are all numbers
|