|
CHAPTER 4 : TRIGONOMETRIC IDENTITIES
IDENTITY : When an equation contains one or more variables and it is valid for all
replacement values of the variable for which both sides of the equation are well defined, then the equation is
known as an identity.
e.g. x2 + 2x + 1= (x + 1)2
But if an equation is true (or valid) for certain replacements of the variables concern, then it is
known as "conditional equation".
e.g. x2 - 3x + 2 = 0
In case of trigonometric equations i.e. equations involving trigonometric functions of
unknown angles, if they are satisfied by all values of unknown angles in their domain of definitions; are known
as identical equations or identities
. While if they are satisfied only by particular values of
unknown angles, they are called as conditional equations or simply equations.
e.g. i) cos x sec x = 1 is an identity since for all values of x it is defined.
ii) sin x = 0 is a conditional equation as for 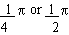 it is not satisfied. it is not satisfied.
We have already seen a number of trigonometric identities. We restate them.
[next page]
|