|
CHAPTER 5 : GRAPHS OF TRIGONOMETRIC FUNCTIONS
5.1 Circular Functions
Functions
A relation from a set A to set B is said to be a function from set A to the set B if each element
of the set A has the relation 'R' with one and only one element of the set B.
For the function f: A ® B, the set A is called the domain of the function
f and B is called the co-domain of the function 'f'. The element y Î
B which corresponds to an element x Î A is called f - image of x
or the value of the function f at x is denoted by f(x) symbolically we
write this as y = f(x). The set of all such (i.e., values of y) is called
the range set of the function f.
Unit Circle
A circle having its radius unity (i.e., 1 unit) and its
centre at the origin of a rectangular coordinate system is
called the "unit circle". If this circle cuts the X-axis in A and
A' and Y-axis in B and B', then we have
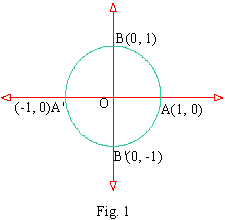
A º (1,0), A' º (-1,0), B º (0,1) and B'
º (0,-1)
If we take P(x, y) be any variable point on this circle,
then by distance formula. OP 2 = (x) 2 + (y) 2 i.e., x 2 + y 2 = 1.
The graph of x 2 + y 2 = 1' is the unit circle.
Now using the notion about a function. We can say that the trigonometric functions are
functions having their domain as the set of
angles and their ranges are sets of real
numbers.
Circular functions are defined such that their domains are sets, numbers and ranges are sets
of real numbers. This definition gives us an analogy between circular and trigonometric functions.
Also, note that the domains of circular functions which are sets of numbers that corresponds
to measures of angles in functions, are sets of real.
The name circular functions is due to the fact that the radian measures of angles are
determined by corresponding actual lengths of the circle.
Thus in the forth coming chapters wherever we define trigonometric functions using unit
circle, leads us directly to these circular functions.
|