|
CHAPTER 6: INVERSE CIRCULAR FUNCTIONS
6.1 Inverse Function
If 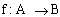 is one-one on to function then corresponding
to every element of B, we can get a unique element of A. This defines a function
from B to A. Such a function is called an inverse function and is defined by is one-one on to function then corresponding
to every element of B, we can get a unique element of A. This defines a function
from B to A. Such a function is called an inverse function and is defined by
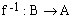
Inverse Circular Functions
Consider the equation 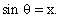 This gives a unique value
of x, for a given value of This gives a unique value
of x, for a given value of 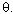 For example if For example if 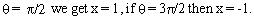 But when x is given , the equation may have no solution or many
(infinite) solutions . If x = 2, there is no solution But when x is given , the equation may have no solution or many
(infinite) solutions . If x = 2, there is no solution 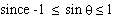 We get infinite values of q but for x >
1, there is no solution.
We get infinite values of q but for x >
1, there is no solution.
For example if sin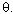 =1/2 ,there are many values of =1/2 ,there are many values of 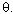 satisfying
the equation, namely satisfying
the equation, namely 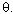 = 300, 1500 , 3900, 5100,..... = 300, 1500 , 3900, 5100,.....
To express 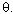 as a function of x, we write as a function of x, we write 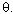 = arc sinx or = arc sinx or 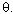 = sin-1x (read
as sine inverse x). = sin-1x (read
as sine inverse x).
It should be noted that sin-1x is entirely different from (sin x) -1
. The former is the measure of an angle in radians whose sine is x while
the latter is 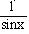
We can similarly define cos-1 x as an angle in radians whose
cosine is x . The other functions of this kind are tan-1x , cot-1x, sec-1x ,
cosec-1x (i.e. csc-1x). These functions are called inverse circular functions
or inverse trigonometric functions.
Principal values
It is at times necessary to consider inverse trigonometric functions as single
valued.
To do this, we select only one value out of many values of angles corresponding
to the given value of x .
This selected value is called the principal value.
1) For sin 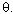 = x or = x or 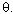 = sin-1x, among all values of = sin-1x, among all values of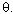 satisfying
this relation, there is only one value between satisfying
this relation, there is only one value between 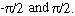 This value of q
is called the principal value of sin -1 x. For example for This value of q
is called the principal value of sin -1 x. For example for 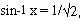 the principal value is
the principal value is 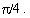 If x is + ve, it lies between 0
and If x is + ve, it lies between 0
and 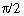 and if x is -ve it lies between - and if x is -ve it lies between - 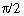 and 0. Therefore the principal
value of sin-1(-1/2) is and 0. Therefore the principal
value of sin-1(-1/2) is 

[next page]
|