|
SUPPLEMENTARY PROBLEMS
1. Find the following : (i) sin-1(-1) (ii) cos-1(1/2) (iii) cos-1(- Ö3/2) (iv) tan -1 (-Ö3) (v) sin -1 (sin 5p/6) (vi) tan -1 (tan 3p/4)
(vii) cos -1 (cos 7p/5)
Ans. (i) -p/2 (ii) p/3 (iii) 5p/6 (iv) -p/3 (v) p/6 (vi) 3p/5
2. Find the general value of each of the following : (i) arc cos 1/2 (p) (ii)
arc tan (- Ö3)
Ans. (i) p/2 + 2np, 5p/3 + 2np (ii) - p / 3 + 2np , 2p / 3 + 2np
3. Find the principal value of each of the following :
(i) Arc cos (-÷2/2) (ii) Arc sin (-1/2) (iii) Arc tan (cot 1) (iv) Arc sec
(- ÷2)
Ans. (i) 3p/4 (ii) -p/6 (iii) p/4 (iv) -3p/4
4. Evaluate (i) Arc sin [cos (-1050)] (ii) Arc tan (cot 2300) (iii) tan (arc
sin00)
Ans. (i) 150 (ii) 400 (iii) 0
5. Prove that (i) 2 arc tan 1/3 = arc tan 3/4 (ii) 2 arc tan 1/3 + arc tan
1/4 = arc tan 16/13
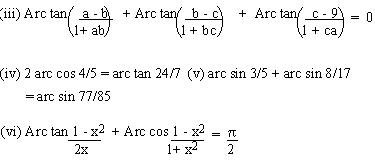
6. Suppose p/2 < x £ p then sin -1 (sin x) = x is not true, using reference angles find m and b in such a way that for p/2 < x £ p, sin -1 (sin x) = mx + b
Ans. -1 andp
7. Solve the following equations :
(1) 2 sin2 q + 3 cos q - 3 = 0
(2) sin 7q - sin q = sin 3q
(3) cos 5q - ÷3 cos 6q + cos 7q = 0
(4) cos q + sin q = cos 2q + sin 2q
(5) 2sin x + cos x = 3 (6) 2 sin2x + 4 sin x cos x = 3
(7) sin 2q = cos 3q (8) ÷3 sec2q + (÷3 + 1) tan q - (÷3 - 1) = 0
(9) cos2x = 1/2 (10) cos x + cos 2x = 0
(11) (tan x -1) (2 sin x + 1) = 0 (12) 2 tan x sin x - tan x = 0
(13) sin 2x + sin 4x = 2 sin 3x (14) sin x / 2 + cos x = 1
(15) sin x / 2 + cos x = 1
(16) If cos (A - B) = 1/2 and sin (A - B) = 1/2 find the smallest + ve of
A and B also their most general solutions.
Answers to Some Questions
(5) p/6, p/2, 5p/6
(9) p/4, 3p/4, 5p/4, 7p/4 (10) p/3, p, 5p/3
(12) 0, p/6, 5p/6, p
(13) 0, p/3, 2p/3, p, 4p/3, 5p/3
(14) 0, p/3, 5p/3
**********
[next page]
|