|
6.2 TRIGONOMETRIC EQUATIONS
Equations involving trigonometric functions of unknown angles are called
1) identities, if they are satisfied by all values of the unknown angles for
which the
trigonometric functions are defined.
2) Conditional equations which are satisfied by particular values of the unknown
angles.
A Solution is a value of the angle which satisfies a given trigonometric
equation.
Solution in a particular interval, such as 0 £ x £ 2p are usually
known as "primary
solution".
A general solution is that formula which lists all possible solutions.
No clear - cut procedure of solving general trigonometric equation exist. It
involves the use of identities, algebraic manipulation, trial and error etc.
Some standard procedures are given below.
1) Factoring (2) Squaring both sides (3) Expressing various functions in terms
of single function .
Example 1
Solve sin x - sin 2x = 0
Solution : sin x - sin 2x = 0

Example 2
Solve : sin 4x - sin 2x = 0
Solution : sin 4x - sin 2x = 0
sin 4x = sin 2x

Now putting n = 0, 1, 2, ... the values of
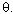 in the range 0 £ in the range 0 £ 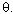 £ 2 p gives the
primary solution. £ 2 p gives the
primary solution.
[next page]
|