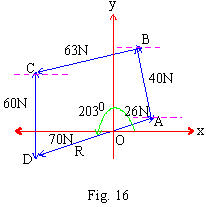
EXAMPLE 4 : Determine the resultant of 26N, 10⁰, 40N, 115⁰, 63N, 188⁰, 60N, 260⁰

Solution

By the Law of Polygon, place tail of each vector in turns at the arrow of the preceding vector.

= Resultant

\ || = 70 N with q_x = 203⁰ (obtained from the measurement of the figure)

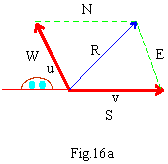
EXAMPLE 5 : A car is traveling due east with the speed of 180 miles per hour. There is a storm, blowing in North west direction at 60 miles per hour. Draw a diagram that represents the car's speed and direction relative to the storm.

Solution

Let V be the velocity vector for car speed with | v | = 180 miles per hour due east.

Let u be the velocity vector for storm speed with |u| = 60 miles per hour due North west

The bearing of v is the angle measured from due north to v is 270⁰ and

The bearing of u is the angle measured clockwise from due north 150

Using tail- up rule, the length and bearing of the resultant calculated as by using Laws of Cosine as

R² = u² + v² - 2uv cos 45⁰

R² = ( 60 )² + (180)² - 2 (60) (180) cos 45⁰

R² = 3600 + 32400 - 2 (21600) (0.7071)

R² = 20726.4935    \ R = 143.97 miles per hour.

Now using Sine Law,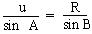

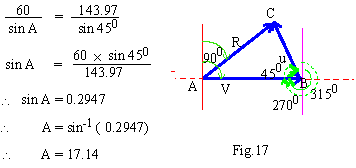
Thus the bearing angle = (90- 17.14)⁰ = 72.86⁰

Index

7.1 Scalers & Vectors
7.2 Algebra of Vectors
7.3 Representation of a vector in a plane
7.4 Dotor Scalar product
7.5 Polar Co-ordinates
Supplementary Problems

Chapter 8