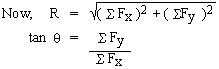NOTE: If a number of forces are acting at a point, the components of all these forces should be found along x- axis and y- axis separately. Then the components along x- axis should be added by considering their signs i.e. algebraically. Similarly components along y- axis should be added algebraically. These sums are called SF_xand SF_y respectively. Then the resultant R is given by

R² = ( SF_x)² + (S F_y)²

The direction of R is found out by the angle. It makes with x- axis in the respective Quadrant. Let it be q then

Procedure of determining R and q

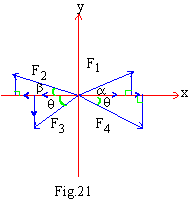
Let F₁, F₂ , F₃ and F₄ are four forces acting as shown in the figure.

S F_x = F₁ cos a - F₂ cos b - F3 cos f + F4 cos q

S F_y = F₁ sin a + F₂ sin b - F₃ sin f - F₄ cos q