Example 37

 Find y’ at the point (1, 0) if xy = log (xy)

Solution :  xy = log (xy). Differentiating w. r. to. x

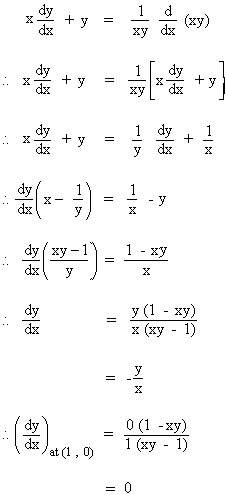
Example 38

If x^p y^p = ( x + y)^p+q Find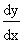

Solution :  x^p y^p = ( x + y)^p+q

Note that here we will use the technique of logarithmic differentiation. i.e. Taking logs of both the sides, we get

p log x + q log y = (p + q) log (x + y)

Differentiating w. r. to x. we get

Chapter 5