|
Example 67
If x = a sec q , y = a tan
q , Find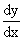 
at q =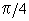 
Solution: x = a sec q
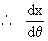= a sec q tan q
and y = a tan q
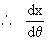= a sec2 q then,
= 
= 
= 
 =
=
=
=
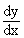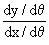
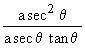
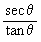
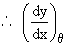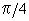
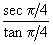
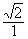
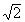
Example 68
If x = a ( q - sin q
) and y = a ( 1 - cos q ). Show that
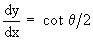
Solution : x = a ( q - sin q
)
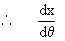= a ( 1 - cos q )
= 
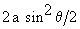
and y = a (1 - cos q)
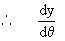= a (sin q)
= 
=
= 
= 
|
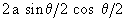
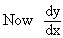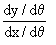
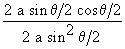
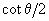
