|
Example 1
Find the equation of the tangent and normal to the curve y = 3x2
- 4x -2 at the point (1, -3)
Solution : y = 3x2 - 4x -2 ®
The curve.
By Differentiating w. r. to x, we get
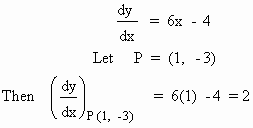
\ Equation of the tangent
at point P (1, -3) is
y - (-3) = 2 (x - 1)
i.e. y + 3 = 2x -2
i.e. y = 2x -5
Next, slope of the normal at
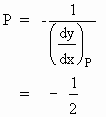
\ Equation of the normal at P
(1, -3) is
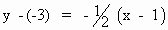
i.e. 2 (y + 3) = - (x - 1)
i.e. x + 2y + 5 = 0
[next page]
|