|
Lagrange’s Mean Value Theorem
It is the generalization of the Rolle’s theorem.
Let f (x) be any continuous function on [a , b] and differentiable
in (a, b), then there exists at least one value of x = c Î
(a, b) such that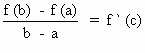 
i.e. f (b) - f (a) = ( b - a) f ' (c)
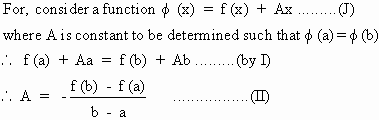
Now f (x) satisfies all conditions of
the Rolle’s theorem. Hence there exists at least one
x = c in (a , b) such that f ' (c) =
0
\ f ' (c) + A = 0 ........(from
I)
\ A = - f ' (c) ............(from
II), we get
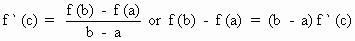
Geometrically - If the graph of y = f (x) is continuous, be drawn between x = a and x = b then A ( a, f (a)) and B (b , f (b)).
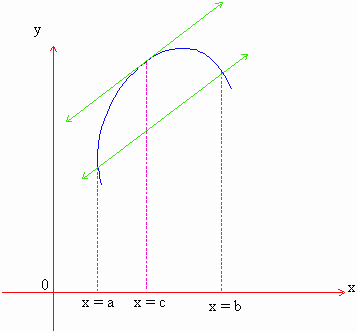
\ Slope of the chord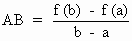 
by L.M.V. , this is equal to the slope of the tangent to y = f (x)
at x = c i.e. f ' (c).
Hence the theorem states that there exists at least one tangent at x =c which is parallel to the chord AB.
[next page]
|
