|
An alternate definition for approximation is as -
If a and a+h belongs to the domain of a differentiable function ’ f ’ , then the approximate value of f (a +h) will be f (a+h) » f (a) + hf ‘ (a), f ‘(a) ¹ 0. By using this, approximate problems can be solved easily.
Example 50
Find correct to 4 decimal places, the approximate
value of 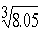
Solution : Let
f (x) = 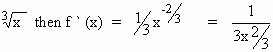
Take a = 8 and h = 0.05 then
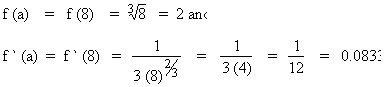
Now the approximation
formula is
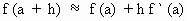
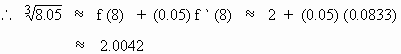
Example 51
Find the approximate value of tan
-1 (0.99)
Solution : Let f (x) = tan-1 (x)
\ f
‘ (x) = 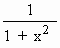
Take a = 1 and h = 0.01 then
f (a) = f (1) = tan
-1 (1) = 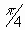 radians. radians.
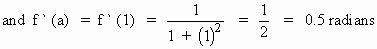
By the approximation formula
f ( a+h ) » f (a) + h f ‘ (a)
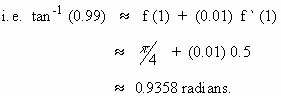
Example 52
Find the approximate value of sin 310
assuming that 10 = 0.0175 radians and cos 300
= 0.8660.
Solution : Let f (x) = sin (x) then f ‘ (x) = cos x
Take a = 300 = p/6 Radians. h = 10 = 0.0175 radians.
Then f (a) = f (300) = sin 300 = 0.5
and f ‘ (a) = f ‘ (30) = cos 300 = 0.8660
using the approximation formula i.e.
f (a + h) » f (a) + h f ‘ (a) we get
\ sin 310 = f (300 ) + ( 0.0175 ) f ‘ (300)
\ sin 310 = 0.5000 + ( 0.0175 ) (0.8660)
\ sin 310 = 0.5152
Errors
Let y = f (x) be a differential function of x and Dx an error in x, then
The approximate error in y is Dy = f ‘ (x) Dx
i.e. Dy = f ‘ (x) dx
Approximate relative
error in y is 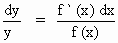
Approximate percentage error in y is
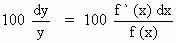
[next page]
|