| 7.5 The
Laws of Probability
So far we have discussed
probabilities of single events. In many situations we come across
two or more events occurring together. If event A and
event B are two events and either A or B or both occurs, is denoted
by A Ç
B or (A + B) and the event that both A and B occurs is denoted
by A Ç B
or AB. We term these situations as compound event or
the joint occurrence of events. We may need probability
that A or B will happen.
It is denoted by P (A Ç
B) or P (A + B). Also we may need the probability that
A and B (both) will happen simultaneously. It is denoted by
P (A Ç B)
or P (AB).
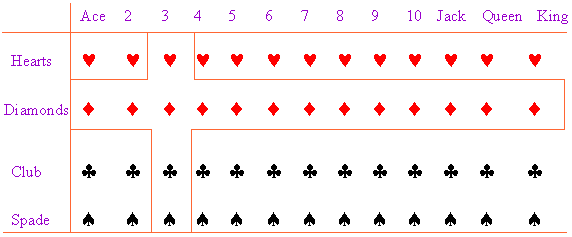
Consider a situation, you are asked
to choose any 3 or any diamond or both from a well shuffled pack of 52
cards. Now you are interested in the probability of this situation.
Now see the following diagram.
It is denoted by P (A È
B) or P (A + B). Also we may need the probability that A and B (both) will
happen simultaneously. It is denoted by P (A Ç
B) or P (AB).
Consider a situation, you are asked
to choose any 3 or any diamond or both from a well shuffled pack of 52
cards. Now you are interested in the probability of this situation.
Now see the following diagram.
Click here enlarge
Now count the dots in the area
which fulfills the condition any 3 or any diamond or both. They are 16.
Thus the required probability 
In the language of set theory,
the set any 3 or any diamond or both is the union of the sets ‘any 3 which
contains 4 cards ’ and ‘any diamond’ which contains 15 cards. The number
of cards in their union is equal to the sum of these numbers minus the
number of cards in the space where they overlap. Any points in this space,
called the intersection of the two sets, is counted here twice (double
counting), once in each set. Dividing by 52 we get the required probability.
Thus P (any 3 or any diamond or
both) 
In general, if the letters A and
B stands for any two events, then
[next page]
|
