|
Formula or Equation :
Consider the function ‘f’ exhibited by the adjoining arrow diagram. 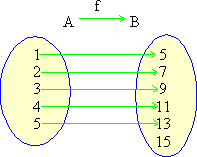
Let A = { 1, 2, 3, 4, 5 }
B = { 5, 7, 9, 11, 13, 15 }
Note that, if we take any element x Î A then the element of the co-domain set B related to x is obtained by adding 3 to twice of x.
Applying this rule we get,
f (1) = 2 (1) + 3 = 5, f (2) = 2 (2) + 3 = 7,
f (3) = 2 (3) + 3 = 9 etc.
In general we can write f (x) = 2x + 3 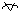 x Î A x Î A
This is the formula which exhibits the function ‘f’ . If we denote the value
of f at x by, y Î B, we get y =
2x + 3 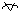 x Î A. This becomes an equation
which exhibits the function f .
x Î A. This becomes an equation
which exhibits the function f .
Remarks :
If a function is exhibited by a formula, then using this formula we can find the range of the function.
Sometimes, the domain is not known or is not given. In such a case, the domain is taken as that set of elements at which the values of the function can be found. For example
-
f(x) = x2 - 3x + 4. In this
case, the set R of all reals is taken as the domain of ‘f’.
-
f(x) = 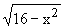 In order to have a real valued function, 16 - x2
³ 0 i.e. - 4 £
x £ 4 which the desired domain
of ‘f ’
In order to have a real valued function, 16 - x2
³ 0 i.e. - 4 £
x £ 4 which the desired domain
of ‘f ’
f (x) = 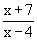 then for x = 4, x + 7 is not defined. Hence in this case, the domain is the x - 4 set R of reals except 4 i.e. R - {4 } then for x = 4, x + 7 is not defined. Hence in this case, the domain is the x - 4 set R of reals except 4 i.e. R - {4 }
Example 1 If A is the area of the circle. Describe this
function.
Solution : If we call this function f then
r is the independent variable and A becomes the dependent variable
and we have A = f(r) = pr2
for r ³ 0
The domain must be stated with the constraint r ³ 0 as we can’t have a circle with negative radius.
|
Index
Introduction
1.1 Functions And Mapping
1.2 Functions, Their Graphs and Classification
1.3 Rules for Drawing the Graph of a Curve
1.4 Classification of Functions
1.5 Standard Forms for the equation of a straight line
1.6 Circular Function and Trigonometry
Chapter 2
|