|
Example 2 A relation is given as : {
(1, 1), (2, ½ ), (3, 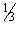 ) , (4, ¼) , (5,
) , (4, ¼) , (5, 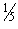 ) } is it a function ? Justify. If it is a function state its domain
and range. Exhibit the relation by a formula.
) } is it a function ? Justify. If it is a function state its domain
and range. Exhibit the relation by a formula.
Solution :
Let A = { 1, 2, 3, 4, 5} and B = {1, ½, 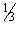 , ¼ , , ¼ , 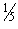 } }
Every element in A occurs once and only once in the ordered pairs and is related
to one and only one element of the set B, exhibiting a relation.
Hence it is a function from the set A to the set B. Let us denote
it by f. Then domain of A = The set A and the range of f = The set
B
Also, the second member in each ordered pair is the reciprocal of the first member. Thus if we denote any element of the set A by x and that of B by y then
The formula is f(x) = 1/x i.e. y = 1/x 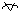 x Î A x Î A
Example 3 A function f is given as f(x)
= x2 - 6x + 5. State its domain. Find f(-2), f(2), f(1),
f(a + h), 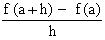 ,h
¹ 0 ,h
¹ 0
Solution :
The domain of 'f ' is the set R of all reals
f(x) = x2 - 6x + 5 Þ
f (-2) = (-2) 2 - 6 (-2) + 5 = 21
f(2) = (2) 2 - 6 (2) + 5 = -
3, f (1) = (1)2 - 6 (1) + 5 = 0
f(a + h) = (a + h) 2- 6 (a + h) + 5 = a2+
2ah + h2- 6a - 6h+ 5
and
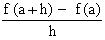
= 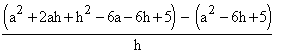
= 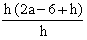
Example 4 Find the range of each of the
following functions
(1) f(x) = 3x + 4 for - 5 £ x £ 8
(2) g(x) = 2x2 + 3 for - 4 £
x £ 3
(3) f (x) = x2-
6x + 7 for all x Î R
Solution :
(1) The domain of ' f ' = { x | x Î R, - 5 £ x £ 8 }
Now -5 £ x £ 8 \
3 (-5) £ 3
(x) £ 3 (8)
\ - 15 £
3x £ 24
\ - 15 + 4 £ 3x + 4
£ 24 + 4
\ - 11 £
f(x) £ 28
The range of ' f ' = { f(x) Î
R, - 11 £ f(x)
£ 28 }
(2) - 4 £
x £ 3 Þ
0 £ x2 £ 16 (why ?
)
\ 2 (0) £
2 (x) £ 2 (16) \
0 + 3 £ 2 x2 + 3
£ 30 + 3
\ 3 £
9(x) £ 35
This is the range of 'g '
|