|
3.2 Continuity In An Interval
1) Let ’f’ be a function defined on (a, b). Then ’f ’ is
said to be continuous on (a, b), if it is continuous at each point
of (a, b).
2) Let ’f’ be a function defined on [a, b]. Then ’f’ is said to be continuous on [a, b] if
i) f is continuous at each point C Î
(a, b)
ii) f is continuous at x = a from right i.e.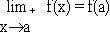
iii)f is continuous at x = b from left i.e.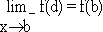
[next page]
|