|
CHAPTER 4 : DERIVATIVES
In this chapter we shall study the derivative, its existence and applications.
We shall be concerned mainly with the real valued functions of a real
variable i.e. the domains and ranges of the functions considered here
will be sets of real numbers.
4.1 Derivability At A Point
Definition :
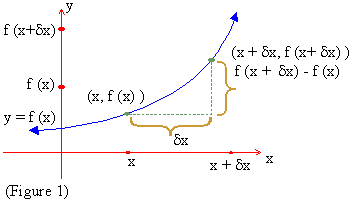
If a function ‘ f ’ is defined by y = f(x) at
a point (x,f (x) ) then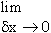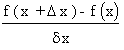  
,
when it exists, is called the derivative of ‘
f ’ at x and this derivative is symbolically denoted by 
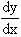or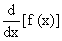 or
f ’(x) or y’ or Df when f ’ (x) exists, we say that ‘ f ’ is derivable
(differentiable ) at x (figure. 1)
\ = 
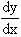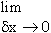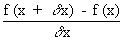
if the limit exists.
The notation ‘dx’
represents a small change in ‘x’.
Now f (x + dx)
- f (x) represents the difference between two values of y = f (x)
viz f (x + dx)
and f (x) and Is denoted by dy
\ = 
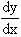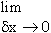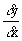
This is called the Leibnitz’s notation and the
detailed definition is as follows.
"If y is a function of
x and when x changes to x + dx,
correspondingly y changes to y + dy,
then the value of the limit, ,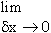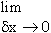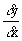
if it exists, is called the derivative of y with respect to x "
and is denoted by .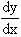
The notation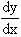
is widely used in all practical work involving derivatives. It is especially used in proving theorems of derivatives.
In particular, the derivative of f at x = a of
its domain, is defined by
f ’ (a) = 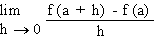 or
by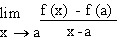 
|
