|
3.5 Discontinuity And Its Classification
A function f(x) is said to be discontinuous for the point x
= c if at least one of three numbers f(c),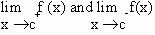 
is different from the other two roughly we have the following types
(a) If x = c and if 
the point is said to have
ordinary or finite discontinuity
(b) If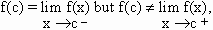 
then ’f’ has ordinary discontinuity on the right.
Similarly if f(c) = lim f(x) but lim f(x, then ’f’
has ordinary discontinuity on the left.
(c) If 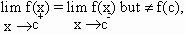 then ’f’ has removable discontinuity at x = c.
The function ’f’ is made continuous at
x = c by assigning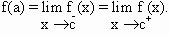 
We shall now illustrate the different types of
discontinuities by using examples.
Consider a function f(x) and a point P whose abscissa is
x = c; then following cases may arise.
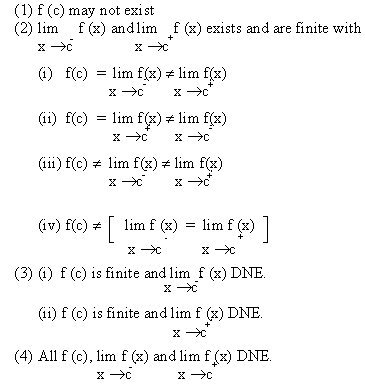
[next page]
|
