|
3.6 Properties Of Functions Continuous On
An Interval
Property 1: If a function f is continuous on [ a, b ], then
the graph of the function is unbroken ( i.e. continuous) curve joining
the points (a, f (a) ) and (b, f ( b))
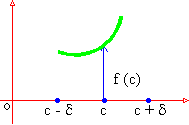
Property 2: If f is the continuous on
[ a, b ] and f ( c ) ¹ 0 and
a < c <
b, then there exists a small positive number d.
So that f ( x ) is of the same sign as f ( c ) then c -
d < x < c + d.
i.e. a continuous function does not undergo sudden
changes. This property will be later on used for the discussion
of Maxima and Minima.
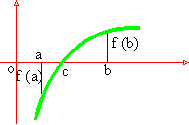
Property 3: If f is continuous on [a
, b] and f (a), f (b) are opposite signs, then f (x) = 0
for at least one value of x in (a , b).
Property 4: If f is continuous on a closed interval
[a , b] then
i) f is bounded in [ a, b ]
ii) There exists points c and d in [ a, b] where f assumes its lub, and glb, M and m respectively.
i.e. f (c) = M and f (d) = m
iii) f assumes every value between m and M at least one value x [ a, b ]
Note :
1) A discontinuous function may be bounded but may not attain the glb or lub.
Even a continuous function on an open interval may not attain glb and lub.
2) These properties are just the necessary conditions but not the sufficient condition to make a function continuous.
**********
[next chapter]
|