3.4 Sum of exterior angles of a Polygon
Figure 3.4
Figure 3.4 shows a pentagon. Its external angles are named from a to e. The aim is to find the sum of these five angles.
It is known that the sum of internal angles of a Pentagon
= (5 - 2 )
´ 1800
= 3 ´
1800
= 540
\ each interior
angle of the pentagon measures
5400 /
5 = 1080
The interior and exterior angles form linear pairs and hence are supplementary.
\ Each exterior
angle measures 1800 - 1080 = 720
\ Sum
of five exterior angles = 5 ´
72 = 3600
It can be proved that the sum of the exterior angles for any polygon is 360 0.
Sum of interior angles of an n sided polygon = ( n - 2 ) 1800.
\ Measure of
each internal angle = 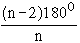
\ Each exterior
angle = 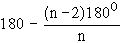
\ Sum of n exterior
angles = 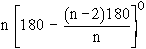
= 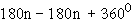
=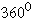
Conclusion : The sum of interior angles of a polygon
is dependent on the number of sides but the sum of the exterior
angles is always 3600.
|